|
A to F G to M N to T U to Z See also: - Arc - Circumference - Diameter - Pi - Radius - Sector - Tangent |
Circle A circle is the locus of a point which moves such that it is a constant distance (the radius, r) from a fixed point (the centre or origin). The circumference, c of a circle is the distance around the edge of the circle. The diameter is the length of the line which passes from one side of the circle to the other, intersecting the centre. The area of a circle is given by 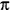 r2, the circumference by 2 r2, the circumference by 2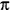 r and the diameter, d by 2r. r and the diameter, d by 2r. 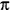 (pi) is given by c/d and is equal to 3.141592654 (to 9 decimal places). (pi) is given by c/d and is equal to 3.141592654 (to 9 decimal places).
An arc is a fraction of the circumference of the circle. A sector is like a slice of cake - a wedge of the circle. 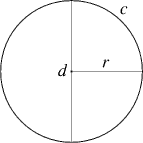
The cartesian equation of a circle with radius r and centre at (a, b) is: (x - a)2 + (y - b)2 = r2. The parametric equation of a circle with radius r and origin (j, k) is: x(t) = r cos (t) + j y(t) = r sin (t) + k The polar coordinates equation of a circle with centre at (c, 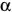 ) and radius a is: ) and radius a is:a2 = 2cr cos ( 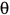 - - 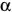 ) + c2 ) + c2
The tangent of a circle is the line running perpendicularly to the radius and touches the edge of the circle at one point only: 
|
Top
[ H O M E ] [ S C I E N C E ] [ M A T H S ] [ A S T R O N O M Y ] [ S E A R C H ]
[ A to F ] [ G to M ] [ N to T ] [ U to Z ]
© 1997 - 1999, Jonathan Stott